Author: Simon Barlovits

Intensive teacher training programme in Granada 2020

Author Simon BarlovitsDate
Events

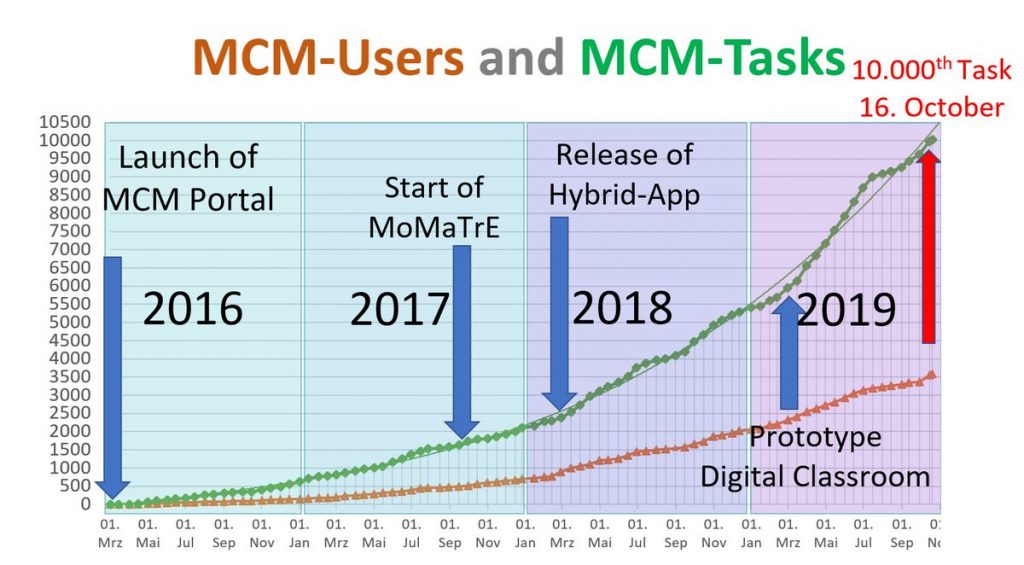
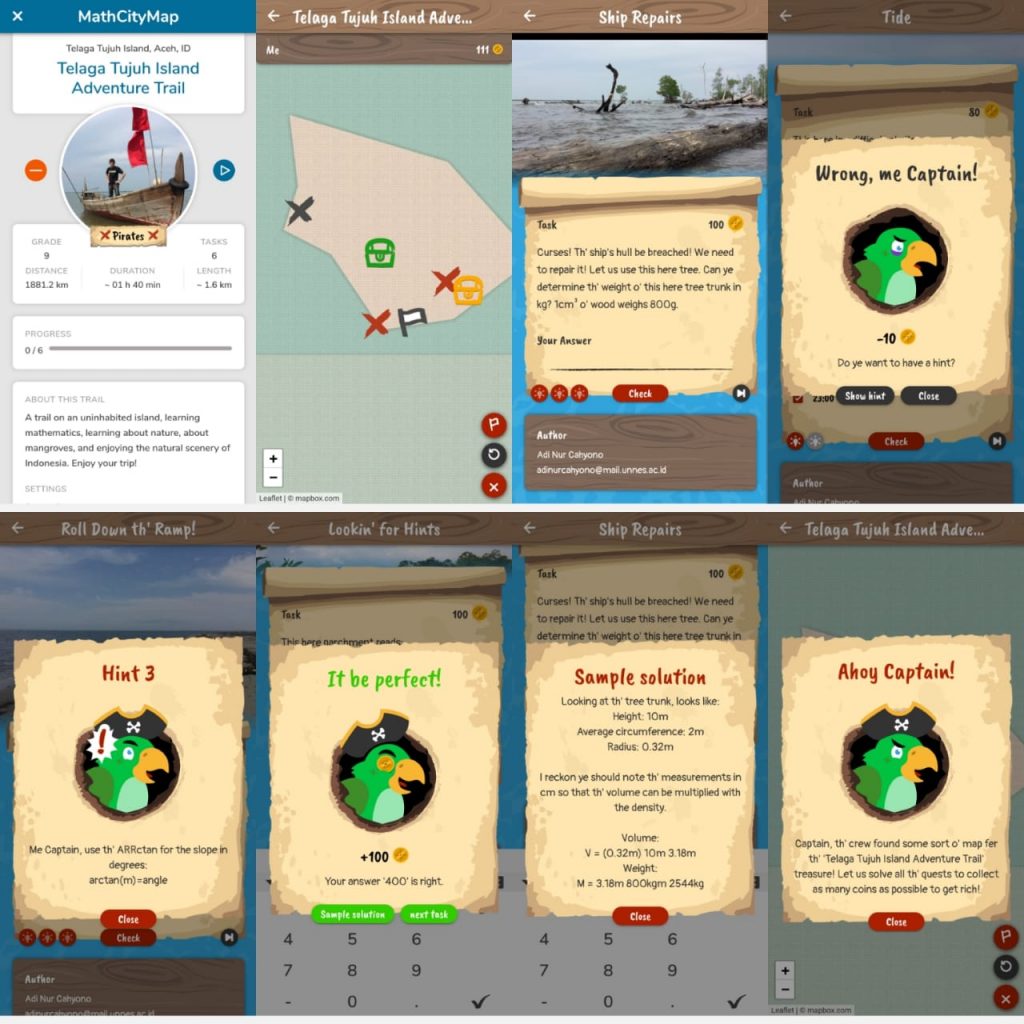
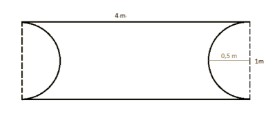
As part of our Erasmus+ Project Mobile Math Trails in Europe (MoMaTrE) you can discover MathCityMap and Outdoor Mathematics with an international group of teachers in the beautiful historic city of Granada!

Do you want to…

  • experience MathCityMap and Outdoor Mathematics in an intensive teacher training programme,
  • work with other teachers and exchange your MathCityMap experiences,
  • visit Granada and do mathematics in a cultural and historical environment?

From 16th to 19th April 2020, a three-day international teacher training will take place in Granada, Spain. During this Multiplier Event, the participants will get to know additional features of the system MathCityMap from different perspectives, create their own tasks and trails and exchange experiences made with the system. We invite all interested teachers to apply for this teacher training.

The event is organized by the Erasmus+ Project MoMaTrE and co-funded by Erasmus+ Programme of the European Union. Through this, the MoMaTrE project can cover the participants’ costs for the conference, accomodation and meals.

Please find all relevant information for the application, on the schedule and the location on the MoMaTrE website!

Task of the Week: So many stairs!

Author Simon BarlovitsDate
Task of the Week

Our new Task of the Week is located in the United States. On the campus of the University of California Santa Cruz the PhD student for mathematics education Julianne Foxworthy created the task “So many stairs!”. She gave us an interview about this task and her usage of MathCityMap.

How did you get in contact with MathCityMap? How do you use MCM?

I discovered the app when I met Iwan Gurjanow [MCM team of the Goethe University Frankfurt] at PME in Sweden last year. I used to teach math to 10-13 year-olds, and I used math trails with them (low-tech version!) and they loved them.

I created the “MBAMP Math Trail“ that this task is a part of for a professional development program for teachers of young students (6-9 year-olds). The teachers were all very interested in using math trails with their students. In the future, I’m planning on creating a series of math trails for various ages at our town’s famous beach boardwalk, so look out for that one!

Please describe your task. How could it be solved?

“So many stairs!” is a very simple task aimed at very young children. The question is, how many steps will you climb altogether, if you and two friends decide to race up the stairs all the way to the door of the library.

The problem solver needs to count all the stairs leading to the library and then, and this will be the tricky part for the youngsters, determine how many stairs will be walked by themselves and their friends.

The teachers who tried the task gave me very helpful feedback about being very clear with my language. The word “step” could be a stair (that’s what I intended) or it could mean a step taken by a person. The second meaning could result in a different answer (e.g., what if a person took the stairs two at a time?).

Task of the Week: Ramp Acess

Author Simon BarlovitsDate
Task of the Week

Todays´ task of the week is located in Portugal, where our MoMaTrE partner Amélia Caldeira created the task “Rampa de Acesso” (engl. Acess Ramp). She answered us some questions about her task and the MathCityMap project.

How do you use MathCityMap?

I use MathCityMap to motivate students to learn mathematics. I want students to be happy to learn and apply mathematics. Through the usage of MathCityMap they can model shapes in the environment. At the same time, I reveal to their teachers a successful recipe for teaching math: technology and outdoor.

Please describe your task and the procedure of solution. What is the underlying problem of your task?

The question of my task “Rampa de Acesso” is, whether the ramp can be comfortably used by a wheelchair person or not. A ramp is rated as wheelchair-assessable, if its slope don`t exceed 6%. The aim of the task is to determine an approximate value for the ramp slope in percentage.

Therefore, the students have to model the ramp (gradient triangle). The slope of the ramp can be calculated as as a ratio between the length and the height of the ramp.

Good to know: MathCityMap provides a wizard task for calculation the slope of a ramp in percent or degree. Wizard tasks are prepared tasks, which can be created only by adding the measured data and a photo of the object.

Task of the Week: Cobblestones

Author Simon BarlovitsDate
Task of the Week

Task of the Week: Cobblestones

This week our Task of the Week is located in Estonia. In the city of Tartu the German mathematics teacher Sascha Abraham created the task “Cobblestones”. In the following he describes his task and the Erasmus project “Making Technology Meaningful Through Digital Pedagogy”, for which he developed this interesting task.

How you get to know the MathCityMap project?

In march I participated in a workshop of MathCityMap. Unfortunately, I didn´t have enough time last school year to work with MCM in math class, but I am going to use the app in this school year. I want to use the tool in two ways. Firstly, I create trails to repeat the educational content before an exam or to illustrate the mathematical content. Secondly, I want that older students create MathCityMap tasks for younger students.

Please describe your task. Why did you create it? How could it be solved?

I created a mathtail and this task within the frame of the Erasmus project “Making Technology Meaningful Through Digital Pedagogy” in order to present MathCityMap to other teachers. The Erasmus project works on the question, how “new technologies” (e.g. electronical devices like tables or smartphones and available software) could benefit mathematical education. In my opinion, MathCityMap enables students to experience mathematical problems in the “real world outside the class room”.

The task cobblestone is an example for a counting task (How many cobblestones are placed in this area?). The task can be solved by calculating how many squared cobblestones at the rectangular area. However, there are two planted areas, wherefore students have to subtract the missing cobblestones. Lastly the students have to add the number of cobblestones, which are placed around the benches. The aim of the task is that students learn to observe their environment carefully in order to solve mathematical problems.

Why do you use wizard tasks?

Wizard tasks are mathematical standard problems, which can be identified nearly anywhere. Through the usage of the MathCityMap wizard users can created a small set of tasks very rapidly. In addition, wizard tasks demonstrate new users different possibilities for interesting mathematical problems.

 

Trail of the Month: Telaga Tujuh Island Adventure

Author Simon BarlovitsDate
General

This month we present a mathtrail from Indonesia. After hearing of the new MathCityMap pirate narrative, our MathCityMap educator Adi Nur Cahyono created the “Telaga Tujuh Island Adventure Trail” to discover this new feature. He gave us an interview about the new pirate narrative feature of MCM.

Why do you use the pirate narrative?

I got the information that there is an app update by adding a pirate narrative in the MathCityMap app, so I immediately searched for a route that matched this narrative. One of which is a route on the Telaga Tujuh Island. The pirate narrative makes my route look very interesting. This narrative fits perfectly with the situation, location and tasks on this route. Adventure at sea, with problems on an island that can only be reached by sailing. It’s like a real pirate, isn’t it?

How could students benefit from the usage of such a narrative?

Students know the pirate character and his adventure stories are looking for treasure. This is the same as math trails ideas. Combining the two makes students interested in exploring the trail by acting like their imaginary character and at the same time they also learn mathematics and its application.

What is the special attribute of your trail? What differentiate your trail from others?

The “Telaga Tujuh Adventure Trail” is a route located on an uninhabited remote island in the Aceh Province of Indonesia. The route is explored by sailing to find some locations and real problems relating to mathematics with pirate narrative, for example, the Ship Repairs task: “Curses! Th’ ship’s hull be breached! We need to repair it! Let us use this here tree. Can ye determine th’ weight o’ this here tree trunk in kg? 1cm³ o’ wood weighs 800g.”

While working on this trail explores discover both mathematics and nature. They learn mathematics while adventurous into the world of imagination in reality and enjoy the beautiful nature of Indonesia. Discover MathCityMap, visit Indonesia!

Good to know: Adi Nur Cahyono created the “Telaga Tujuh Island Adventure Trail” in order to discover our new pirate narrative. Therefore, the used a lot wizard tasks of this trail, because the MCM provides for each of these tasks a short story fitting to the pirate narrative.

MathCityMap visits Namibia

Author Simon BarlovitsDate
EventsGeneral

Matthias Ludwig presents the MathCityMap project in Namibia!

At J.G. Van der Wath Secondary School Matthias Ludwig created some MathCityMap tasks with Namibian teachers during a teacher education program. One of these new tasks is “The tire”, for which students have to calculate the circumference of a semi-visible car tire.

The participants of the education program were highly interested in the MathCityMap idea – so we are looking forward to a lot of interesting task which hopefully will be created soon!

You can find photos and further information on our MCM Twitter site.

Task of the Week: Flower Frame

Author Simon BarlovitsDate
Task of the Week

Todays´ task of the week was created in Druskininkai, Lithuania, by our MoMaTrE project partner Sona Ceretkova. The aim of the task is to explore a flower frame and to calculate the missing percentage of the frame. Sona Ceretkova gave us an interview about this interesting task.

What´s the topic of the task?

The frame for the task is situated in Lithuania, spa town Druskininkai, which is flowers paradise itself. It is quite common gardening practice to frame a piece of lawn by stones or bricks and plant some nice composition of flowers inside the area of the frame. The flower frame chosen for the task is an interesting geometrical shape. rectangle with shorten sides cut.

Several mathematics calculations can be presented of the flower frame:

  1. Calculate the inner area of the complete frame (without cuts).
  2. Calculate the area of cut parts.
  3. Calculate the difference between the area of the whole frame and cut parts.
  4. Calculate the ratio of whole frame and cut parts.
  5. Calculate the ratio of the cut frame and cut parts.
  6. Calculate the missing percentage of the whole frame.
    This is the given task in Druskininkai.

How could you solve this problem?

The original frame has “mathematically friendly” measures with a length of 4 metres and a width of 1 meter. The cut parts are two identical semi-discs, which create one whole disc (in calculation). This information is given by a hint. The geometrical situation of the task is quite simple (see figure).

Another hint declares that the area of the whole rectangle is 100%. This hint is an important note for correct calculation of the percentages. Since the exact percentage calculation gives 19,625%, rounding of this number was other mathematical skill required by solvers.

The multiple choice is the most suitable alternative as the answer. It´s an interesting game to ask solvers about their estimation of the tasks` solution. The 20% (one fifth) is a quite large number, quite large part, which is cut of the whole area of the flower frame. It is not so obvious when observing and measuring the real object.

What´s the didactic aim of the task?

We want to stimulate the following didactics aims through the task.

  1. Measure precisely.
  2. Imagine, draw or describe an ideal geometrical situation: rectangle, semi-circle (semi-disc).
  3. Calculate areas of two basic geometric shapes: rectangle and circle (disc).
  4. Use units in correct way; square meters are recommended.
  5. Calculate number of percentages when knowing the base and the percentage part.
  6. Interdisciplinary approach: ecology & botany

Task of the Week: The weight of DCU

Author Simon BarlovitsDate
Task of the Week

This week our presented task is located in Ireland. At the campus of the Dublin City University (DCU) our MoMaTrE partner Christian Mercat created the task “The weight of DCU” and gave us an interview about this task and the value of using the MathCityMap app.

What´s the topic of the task?

On the campus you can find a huge DCU solid rock sign. I really wondered how much that could weight! So I investigated and figured out that one could estimate the surface of the letters and the depth of the sculpture.

How could you solve this problem?

You have to estimate the average width of the letters and their lengths. For example, C is a 2/3 portion of a circle of diameter 2 m and average with 30 cm. So is has a surface of 1.2 m². The modelling of D and U happens equally. Totally the sculpture has a surface of 4.5 m². The depth of the stone is 50 cm, which leads to a total volume of 2.25 m³. The density of the stone being 2.4 (that’s given in the first hint), the total weight of the sculpture is around 5400 kg. The estimation of the surface being tricky, I actually checked again by taking a picture from a distance and estimating numerically the total surface with the help of my computer. 

Estimation of the sculptures` surface.

What´s the didactic aim of the task?

Clearly, I want here to get first the students to have a rough estimation of the degree of magnitude, is it around hundreds of kg, a few tons or tens of tons. I give a broad « orange » zone between 3000 and 7500 kg for those trying to figure out by simply bracing their arms around the sculpture to get a sense of the volume, which I find fair enough for an answer. But then, trying to model each letter as simpler geometric shapes is really the main focus of this task. It can not be done exactly, the average width of each letter is a matter of debate, which is good. The « green » zone might be a little bit too tight (between 5000 and 6000) which is only a 20% width around the expert estimation, but the depth is without any doubt 1/2 meter so the uncertainty really is on the surface estimation.

Why do you use MathCityMap?

I love taking the pretext of a MathCityMap trail in order to stroll around on a campus or in a park, appreciating the scenery from this very specific perspective of looking around for objects that tickle my mathematical inclination, keeping open the scientific eye in me.

Task of the Week: The green ear

Author Simon BarlovitsDate
Task of the Week

Today´s task of the week is located in Lüneburg, Germany, where the teacher trainee Jennifer Oppermann created the task “The green ear”. She gave us an interview about this task, mathematic modelling and the MathCityMap project.

What´s the topic of the task?

The question is, how tall the human being would be, the green ear belongs to. To solve the task students first have to measure the sculpture of the green ear, followed by measuring an ear of a student. In addition, the body size of this students should be identified.

Afterwards the quotient of the length of the green ear and the students´ ear is multiplicated with the body height of the student. Thereby the size of the human being, to whom the green ear would belong, can be estimated.

What´s the didactic aim of the task?

While working on the task, students should improve their competences in mathematic modelling. Modelling means to link the reality and the mathematic and to solve a given problem through a mathematic calculation. Thus, MathCityMap is a helpful tool to observe the connection between environment and mathematics and to exert mathematical strategies.

How do you use MathCityMap?

To discover our near environment out of a mathematical perspective, we created a math trail through the Hanseatic town of Lüneburg. The MathCityMap project enables mathematic interested people to solve our tasks around Lüneburg and to increase their mathematical competences.