“Math Doer” of the month June 2018 are the people behind MathCityMap. The idea of their app: Students walk around the area and solve measuring and arithmetic tasks at several stations that are provided by the app. There is almost nothing that cannot be used as a trail object. Sometimes they measure tree trunks to calculate their age, or how fast the steps of an escalator run. The students immediately see on the screen of their smartphone whether they are right. You also see that in many things there is a lot of mathematics and it is basically very concrete. Thousands of users, mostly teachers, have created their own nature trails and shared them on mathcitymap.eu. Here, project manager Matthias Ludwig gives a look behind the scenes and reveals how the MathCityMap team wants to force its competitor Pokémon Go.
Mr. Ludwig, how did you come up with the idea for MathCityMap?
As I was still teaching, I liked to lead my students away from the textbooks, out of the classroom, into the real world. With measuring and writing equipment, we walked through Würzburg’s vineyards and measured grapevines, the slope, a pond in the park or other objects in the city. A kind of outdoor station learning, whereby the students playfully gained a look for the mathematics in the things and always experienced a little adventure. The idea of the mathematical trails came up in England in the 1980s. The usual tasks at the time were various: determine water speed, count combinations, and so on. Too various for a lesson. With MathCityMap we adapt trails in terms of content and time to lessons and into the twenty-first century. The mobile technologies offer new possibilities: better distribution and exchange, assistance and direct feedback on solutions. It forms a large community. Everyone can basically join in, even get creative and design and share their own trails. In addition, we can also explore the learning effects, because we link recorded data with students’ handwritten notes.
Why do you want that?
One question was how to make smartphones useful in class. So far, the literature includes more qualitative assessment of the trails à la it is great, makes fun. We conduct evaluation studies to capture the didactic benefit. For example, we found that gamification is beneficial. The students are more motivated when competing in groups for points. Otherwise, you tend to guess results. The bottom line is that it is a win-win-win situation: students are more motivated and on average learn better than the control group in the classroom, teachers have material and variety, and we learn how good the whole thing is.
How does a place become mathematically interesting?
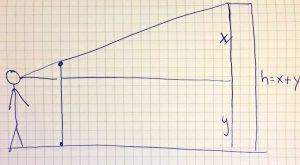
It always depends on the creativity of the user. It may be the most trivial things that are usually ignored: the pavement in the pedestrian zone, which symmetry does it have? How many paving stones are on this place? The bus stop on our street, how likely will the bus arrive in the next five minutes? The tree in the schoolyard, how old is it? This is proportional to the diameter in a certain age range. Or the statue in the fountain, which mathematical shoe size does it have? Of course you can exaggerate this with figures of the environment. Therefore, and as a kind of interdisciplinary link, we use “sidefacts” in the app, which tell a little about the history of the places.
The tasks often focus on geometry and surveying …
Yes, geometry is strongly represented. Once because it fits the school content. Then lengths, areas, gradients are practically measured and are also in the literal sense obvious, more than a probability. These schemes also spread more, because they work almost everywhere and we provide technical support when creating: With the task wizard or generic tasks, it is possible to pick up a schema and create it for my city in just a few clicks. But measuring is not everything. On the way to solution, one also has to apply equations correctly, solve for variables and calculate with units. If the volume of a stone is required, one has to model it mathematically, find the appropriate elementary geometric body. But also questions of analysis, combinatorics, and soon also of analytic geometry occur.
Who is MathCityMap aimed at?
Recreational mathrailers are more the exception. As a mathematics didactics, we mainly take care of the school area and lessons. We know that teachers are under pressure and have little time for additional preparation. We try to make it as easy as possible for them.
Do you check the trails created by users?
You can create private trails that only your students can access via code. There, the quality is simply ensured by your competence and the required input fields – solution hints, solution, photo, coordinates, etc. If you want to share the trail with the whole world, our team checks before the publication whether everything is consistent and technically perfect. This is going well, also thanks to our competent project partners worldwide, who check trails in other countries. And the network is growing.
Sounds like a viral success.
Well, still we are not a serious competitor for Pokémon Go, an app with the same gaming concept. But for people who want to get away from that stuff, we will set up distribution points for our “Mathadon”. Joking aside, there are over three thousand tasks and more than five hundred trails in eleven languages. We plan MathCityMap institutes, where further education for teachers, trail authors etc. should take place. The international exchange is enormously inspiring. I always thought I had a lot of imagination, but I always meet people who top that easily. They would create a good trail in the desert, too. That’s great! At the end of the funding period through the EU, 2020, we are making a big congress. And hope for renewal.
Thank you very much for the interview, Mr. Ludwig, and all the best for your team and MathCityMap!