In dieser Woche möchten wir Ihnen in der Rubrik Aufgabe der Woche gleich eine ganze Reihe von Aufgaben vorstellen. Mathias Bärtl, Professor an der Hochschule Offenburg, ist auf MathCityMap aufmerksam geworden und hat das System für Studierende seiner Statistikvorlesung angepasst, beispielsweise in der Aufgabe „Werbeflächen in der U-Bahn“.
Aufgabe: Werbeflächen in der U-Bahn
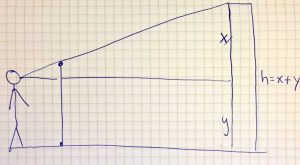
ONE STEP AHEAD Fitness möchte Messebesucher vor allen anderen auf sich aufmerksam machen und eine Werbefläche an der Haltestelle „U2 Messehallen“ anbringen, an der Rolltreppe zur „Karolinenstraße – Marktstraße – Hamburg Messe“. Würde sich das rentieren? Nehmen wir an, dass sich eine Flächenwerbung im Durchschnitt 25 Sekunden im Sichtbereich eines Menschen befinden muss, bevor er sie wahrnimmt, und dass dieser Sichtbereich hier zwischen dem ersten und vorletzten Nothalt-Griff liegt. Berechnen Sie die Wahrscheinlichkeit, mit der dann ein ankommender Besucher unsere Werbung bemerken würde! Geben Sie das Ergebnis als ganze Prozentzahl an (also z.B. 25, wenn Ihre Berechnung 0,252 ergeben sollte).

Mithilfe der Rolltreppengeschwindigkeiten und der Expontentialverteilung als Verteilungsfunktion können die Studierenden die Aufgabe lösen. Im Interview gibt Mathias Bärtl selber einen Einblick hinter die Idee MathCityMap für Studierende zu nutzen.
- In welchem Kontext haben Sie MathCityMap eingesetzt? Wie sind Sie auf das Projekt aufmerksam geworden?
Die MathCityMap habe ich im März 2018 auf der gemeinsamen Jahrestagung der GDMV in Paderborn kennengelernt. Allerdings wie so oft nicht in einer Veranstaltung, sondern in einem beiläufigen Gespräch mit dem Erfinder der App im Bus zur Tagungsstätte. Die Kombination aus digitalen Medien, Stadterkundung und Arbeit im Team an konkreten Objekten hat mich sofort begeistert. Ich konnte mir gut vorstellen, dass sich auch Studierende von der App angesprochen fühlen, wenn man sie mit etwas anspruchsvolleren Aufgaben herausfordert. Für mich eröffnet sich damit eine gute Möglichkeit, Inhalte der Statistik-Vorlesung in praktischen Situationen und motivierender Umgebung anwenden zu lassen.
- Welche Inhalte und Kompetenzen kommen in Ihrem Trail vor? Welche Zielgruppe wird angesprochen?
Der Trail versetzt die Teilnehmer – Studierende wirtschaftsbezogener Fächer – in die Situation eines Projektmanagers, der die Markteinführung von Fitnessgeräten vorbereiten soll. Hierzu müssen verschiedene Orte Hamburgs aufgesucht und unter bestimmten Fragestellungen analysiert werden. Mein Augenmerk bei der Entwicklung lag darauf, Inhalte der Statistikveranstaltung aufzugreifen und in eine in sich stimmige Gesamtgeschichte einzubetten, die gleichzeitig die Erkundung spannender Orte verlangt. Ich habe daher zugegebenermaßen nicht primär mit der Definition gewünschter Kompetenzen begonnen. Letztlich sind die entwickelten Aufgaben aber der mathematischen Modellierung und Lösung zuzuordnen. Inhaltlich werden die Bereiche Wahrscheinlichkeitsrechnung, Schätzen und Testen, aber auch Korrelation und Regression abgedeckt.
- Haben Sie den Trail bereits getestet und Feedback erhalten?
Ich habe einen Testlauf mit zwei Studierenden durchgeführt. Dabei ging es mir um ein Erproben der Verständlichkeit und Machbarkeit der Einzelaufgaben sowie eine Prüfung des zeitlichen Ansatzes. Als Test unter wissenschaftlichen Gesichtspunkten kann man das natürlich nicht werten. Die beiden Teilnehmer waren extrem motiviert und Feedback wie „Es hat richtig viel Spaß gemacht! Ich denke, dass es bei Studenten einen positiven Eindruck hinterlassen wird.“ verspricht, dass die Idee auch im größeren Stil gut ankommen wird. Ich freue mich jedenfalls darauf, das Ganze zukünftig als Wahlpflichtfach mit Exkursion anzubieten.
Wir danken für das Interview und die tolle Umsetzung der MathCityMap Idee in neuem Kontext.