Simone Jablonski – Seite 4

4000. MathCityMap Aufgabe im Portal

Bei dem anhaltenden sommerlichen Wetter ist es eigentlich kein Wunder, dass es die Mathtrailer nach draußen zieht. Wir freuen uns besonders darüber, dass in dieser Woche die 4000-Aufgaben-Grenze im Portal überschritten wurde. Outdoor Mathematik mit MathCityMap rund um den Globus haben wir aktuell rund 1500 Usern zu verdanken. Zusammen wurden über 600 Routen in 17 […]

Bei dem anhaltenden sommerlichen Wetter ist es eigentlich kein Wunder, dass es die Mathtrailer nach draußen zieht. Wir freuen uns besonders darüber, dass in dieser Woche die 4000-Aufgaben-Grenze im Portal überschritten wurde.

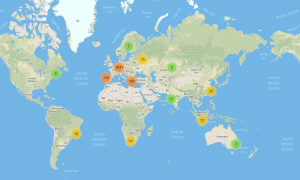
Outdoor Mathematik mit MathCityMap rund um den Globus haben wir aktuell rund 1500 Usern zu verdanken. Zusammen wurden über 600 Routen in 17 verschiedenen Ländern angelegt. Beachtliche Anteile daran haben neben unseren internationalen Kooperationspartnern von MoMaTrE und dem MOOC der Universität Turin auch die vielen engagierten und motivierten Aufgabenersteller, die MathCityMap an ihrer Schule, Universität oder in ihrer Freizeit nutzen. An dieser Stelle vielen Dank!

Das Projekt hat damit eine wie wir finden tolle Entwicklung hingelegt und lässt uns bereits einige Zukunftspläne schmieden.

Aufgabe der Woche: Pflastersteine

Im Rahmen der ICM Konferenz in Rio de Janeiro hat Iwan Gurjanow erste Aufgaben auf südamerikanischem Boden angelegt. Im daraus entstandenen Trail findet sich auch unsere heutige Aufgabe der Woche wieder. Aufgabe: Pflastersteine (Aufgabennummer: 4505) Wie viele Pflastersteine befinden sich annähernd in der rot markierten Fläche? Während wir die Aufgabe bereits häufig bei kreisförmigen oder […]

Im Rahmen der ICM Konferenz in Rio de Janeiro hat Iwan Gurjanow erste Aufgaben auf südamerikanischem Boden angelegt. Im daraus entstandenen Trail findet sich auch unsere heutige Aufgabe der Woche wieder.

Aufgabe: Pflastersteine (Aufgabennummer: 4505)

Wie viele Pflastersteine befinden sich annähernd in der rot markierten Fläche?

Während wir die Aufgabe bereits häufig bei kreisförmigen oder rechteckigen Flächen angelegt haben, kommt an dieser Stelle das Parallelogramm ins Spiel. Denn es bieten sich an, den Flächeninhalt zu bestimmen und die Anzahl der Steine in einem gewissen Bereich zu zählen, z.B. in einem mit dem Zollstock ausgelegten Quadrat der Größe 60×60 cm. Diese Anzahl wird dann auf die Gesamtfläche hochgerechnet, deren Flächeninhalt sich schnell über Seitenlänge und Höhe des Parallelogramms ergibt.

Eine zeitsparende Variante zum mühsamen Zählen, denn so viel sei verraten: Die Lösung liegt bei weit über 1000.

Aufgabe der Woche: Himmelsrichtung

Mit unseren GPS-Aufgaben, wie dem Ablaufen einer Nord-Süd-Strecke haben wir bereits eine erste Möglichkeit vorgestellt, wie man die Himmelsrichtungen mit MathCityMap verbinden kann. Doch auch viele Statuen bieten die Möglichkeit, das Thema umzusetzen. So zum Beispiel das Denkmal von Maximilian Churfürst von Bayern in München. Aufgabe: Fingerzeig des Maximilians (Aufgabennummer: 3161) In welche Himmelsrichtung zeigt […]

Mit unseren GPS-Aufgaben, wie dem Ablaufen einer Nord-Süd-Strecke haben wir bereits eine erste Möglichkeit vorgestellt, wie man die Himmelsrichtungen mit MathCityMap verbinden kann. Doch auch viele Statuen bieten die Möglichkeit, das Thema umzusetzen. So zum Beispiel das Denkmal von Maximilian Churfürst von Bayern in München.

Aufgabe: Fingerzeig des Maximilians (Aufgabennummer: 3161)

In welche Himmelsrichtung zeigt der rechte Zeigefinger von Maximilian? Gib das Ergebnis in Grad an. Wobei 0° der exakten Nordrichtung und 90° der exakten Ostrichtung entsprechen.

Mit Einsatz des Smartphones und zugehöriger Kompass-App lässt sich die Aufgabe ganz schnell und exakt lösen. Ohne Kompass wird ein bisschen Kreativität verlangt. So lässt sich die grobe Himmelsrichtung mithilfe des Sonnenstandes oder der nach Norden gerichteten Mathtrail-Karte bestimmen. Wenn im Vorfeld klar ist, dass die SchülerInnen ohne Kompass arbeiten sollen, bietet es sich an, die Fragestellung auf die Himmelsrichtung mit Multiple-Choice einzugrenzen.

Aufgabe der Woche: Diogenes und sein Fass

Mathematik vor traumhafter Kulisse machen – das verspricht die aktuelle Aufgabe der Woche zur Statue von Diogenes von Sinope. Als einflussreicher antiker griechischer Philosoph bekannt, wird ihm nachgesagt ohne festen Wohnsitz und stattdessen des Öfteren in einem Fass genächtigt zu haben. Diese wird der Kern unserer mathematischen Berechnungen. Aufgabe: Diogenes und sein Fass (Aufgabennummer: 4467) […]

Mathematik vor traumhafter Kulisse machen – das verspricht die aktuelle Aufgabe der Woche zur Statue von Diogenes von Sinope. Als einflussreicher antiker griechischer Philosoph bekannt, wird ihm nachgesagt ohne festen Wohnsitz und stattdessen des Öfteren in einem Fass genächtigt zu haben. Diese wird der Kern unserer mathematischen Berechnungen.

Aufgabe: Diogenes und sein Fass (Aufgabennummer: 4467)

Bestimme das Volumen des Fasses, in dem Diogenes lebt. Gib das Ergebnis in Litern an.

Wie lässt sich nun das Fass am besten durch bekannte geometrische Körper beschreiben? Sicherlich kommen verschiedene Modelle in Frage. Ein hinreichend genaues Modell ist die Verwendung von zwei Kegelstümpfen, wobei jeweils die Grundflächen mit dem größeren Radius in der Mitte des Fasses aneinanderliegen.

Die Höhe ergibt sich leicht durch Messung der Höhe des Fasses geteilt durch 2. Mithilfe des Umfangs lässt sich in der Mitte des Fasses und am unteren/oberen Ende jeweils der kleine und große Radius bestimmen. Hierbei können auch die regelmäßigen Streben am Fass helfen.

Mithilfe der Formel für einen Kegelstumpf ergibt sich dann das angenäherte Volumen für das gesamte Fass.

Aufgabe der Woche: Wirbel

Dass die Münsteraner Innenstadt viele Aufgabenstellungen bereithält, wird mit einem Blick auf die Portalkarte schnell deutlich. Auch im Trail rund um den Aasee zeigt sich Münster von einer vielfältigen mathematischen Seite. Aufgabe: Wirbel (Aufgabennummer: 431) Das Kunstwerk von Henry Moore aus dem Jahr 1974 stellt mehrere idealisierte Wirbel (lat. vertebrae) dar. Diese Wirbel stehen absichtlich […]

Dass die Münsteraner Innenstadt viele Aufgabenstellungen bereithält, wird mit einem Blick auf die Portalkarte schnell deutlich. Auch im Trail rund um den Aasee zeigt sich Münster von einer vielfältigen mathematischen Seite.

Aufgabe: Wirbel (Aufgabennummer: 431)

Das Kunstwerk von Henry Moore aus dem Jahr 1974 stellt mehrere idealisierte Wirbel (lat. vertebrae) dar. Diese Wirbel stehen absichtlich nah, aber doch unverbunden beieinander. Stelle dir vor, man würde sie zusammenfügen und als Teil der menschlichen Wirbelsäule eines Erwachsenen sehen. In der Realität ist ein durchschnittlicher Wirbel eines 1,80 m großen Erwachsenen ungefähr 2 cm lang. Schätze, wie groß ein Riese wäre, dessen Wirbelsäule aus Wirbeln dieser Größe bestände (in m).

In dieser Aufgabe wird insbesondere das Schätzen und Modellieren betont. Durch die Angabe in der Aufgabenstellung kann mithilfe der Wirbellänge am Kunstobjekt eine Referenzgröße bestimmt werden. Eine entsprechende Messung und Berechnung mithilfe des Verhältnisses liefert die gesuchte Größe.

Nach einem Mathe-Tag des P-Seminars Mathematik der Theodosius-Florentini-Schule Gemünden gibt es einen Artikel über MathCityMap in der örtlichen Zeitung Mainpost. Lesen Sie hier den Artikel.

Aufgabe der Woche: Höhe der Skulptur

Zu Beginn des Monats hat Iwan Gurjanow das MathCityMap Projekt erfolgreich in Schweden auf der PME Konferenz vorgestellt. Natürlich wurden vor Ort auch Aufgaben angelegt, so wie die heutige Aufgabe der Woche. Aufgabe: Höhe der Statue (Aufgabennummer: 4303) Wie hoch ist die Statue? Gib das Ergebnis in Metern an. Die Aufgabe lässt sich auf verschiedene […]

Zu Beginn des Monats hat Iwan Gurjanow das MathCityMap Projekt erfolgreich in Schweden auf der PME Konferenz vorgestellt. Natürlich wurden vor Ort auch Aufgaben angelegt, so wie die heutige Aufgabe der Woche.

Aufgabe: Höhe der Statue (Aufgabennummer: 4303)

Wie hoch ist die Statue? Gib das Ergebnis in Metern an.

Die Aufgabe lässt sich auf verschiedene Arten lösen. Zum einen ist es aus einer größeren Entfernung möglich, mithilfe einer Person als Referenzgröße zu schätzen, wie oft diese Person in die Statue passt.

Genauer wird es, wenn die Aufgabe mithilfe des Strahlensatzes gelöst wird, wie im folgenden Hinweisbild dargestellt:

Als Referenz kann hier der Zollstock dienen.

Aufgabe der Woche: Säulen im Park

Diese Woche gibt uns Carmen Monzo, Lehrerin in Spanien, einen Einblick in ihre Aufgabe „Säulen im Park“. Die Aufgabe wurde in einem Park in Albacete erstellt, der „viele mathematische Elemente enthält, die die Leute nicht wahrnehmen, solange sie nicht die mathematische Brille aufhaben.“ Task: Säulen im Park (Task Number: 3981) Bestimme die Oberfläche (in m²) […]

Diese Woche gibt uns Carmen Monzo, Lehrerin in Spanien, einen Einblick in ihre Aufgabe „Säulen im Park“. Die Aufgabe wurde in einem Park in Albacete erstellt, der „viele mathematische Elemente enthält, die die Leute nicht wahrnehmen, solange sie nicht die mathematische Brille aufhaben.“

Task: Säulen im Park (Task Number: 3981)

Bestimme die Oberfläche (in m²) einer der Säulen.

„Ich mag insbesondere diese Stuktur. Parallele and senkrechte Linien können einfach gefunden werden, ebenso wie die Säulen (Zylinder), deren Oberfläche einfach mithilfe eines Zollstocks oder Maßbands und einem Taschenrechner bestimmt werden kann. Die Höhe des Zylinders kann einfach bestimmt werden, aber für eine möglichst genaue Bestimmung des Radius‘ am Boden, müssen die Schüler zunächst den Umfang messen und durch 2 Pi dividieren.

Da es zwölf Säulen gibt, can die Aufgabe simultan von etwa 20 Schülern bearbeitet werden. Anschließend können sie ihre Ergebnisse vergleichen und über die Wichtigkeit der Messgenauigkeit nachdenken. Um die Aufgabe zu lösen ist Wissen über 2D und 3D Formen, das Konzept der Oberfläche und Formeln zur Berechnung notwendig.

Als Sekundarstufen Mathematiklehrerin denke ich, dass unsere Schüler verschiedene Aktivitäten wie messen, zählen, fühlen und mit ihren Sinnen arbeiten durchführen sollten. MathCityMap gibt Schülern und Lehrern die Motivation solche Dinge mit moderner Smartphone Technologie zu betreiben.

MathCityMap auf dem New Horizons in Teaching Science Workshop in Italien

Am 18. Juni 2018, fand der the „New Horizons in Teaching Science“ in Messina auf Sizilien statt. Bei diesem Anlass stellte Eugenia Taranto das MathCityMap Projekt und die Kooperation mit dem Matheprojekt MOOC UniTo (Massive Open Online Course Universität Turin). Viele verschiedene Aufgaben, die im Rahmen des MOOC „Verhältnis und Funktionen“ von sizilianischen Lehrern erstellt […]

Am 18. Juni 2018, fand der the „New Horizons in Teaching Science“ in Messina auf Sizilien statt.

Bei diesem Anlass stellte Eugenia Taranto das MathCityMap Projekt und die Kooperation mit dem Matheprojekt MOOC UniTo (Massive Open Online Course Universität Turin).

Viele verschiedene Aufgaben, die im Rahmen des MOOC „Verhältnis und Funktionen“ von sizilianischen Lehrern erstellt wurden, konnten gezeigt werden.

Es zeigte sich vielseitiges Interesse und wir hoffen, dass die Zahl an sizilianischen und italienischen Aufgaben weiterhin wachsen wird!

Aufgabe der Woche: Vordach

Die klassischen geometrischen Körper und Figuren sind in der Umwelt vielzählig zu finden. Dennoch weichen reale Objekte vom idealen Körper ab und erfordern Modellierungskompetenzen. Daneben sind zusammengesetzte Körper keine Seltenheit. So auch in unserer aktuellen „Aufgabe der Woche“, die von Bente Sokoll, Schülerin am Johannes-Brahms-Gymnasium in Hamburg erstellt wurde. Aufgabe: Rauminhalt unter dem Vordach (Aufgabennummer: […]

Die klassischen geometrischen Körper und Figuren sind in der Umwelt vielzählig zu finden. Dennoch weichen reale Objekte vom idealen Körper ab und erfordern Modellierungskompetenzen. Daneben sind zusammengesetzte Körper keine Seltenheit. So auch in unserer aktuellen „Aufgabe der Woche“, die von Bente Sokoll, Schülerin am Johannes-Brahms-Gymnasium in Hamburg erstellt wurde.

Aufgabe: Rauminhalt unter dem Vordach (Aufgabennummer: 3907)

Berechne das Volumen unter dem Vordach (wenn die Seiten geschlossen wären). Gib das Ergebnis in m³ an.

Um das Volumen zu berechnen, wird der Körper in einen Quader und zwei halbe (idealisierte) Zylinder geteilt. Für den Quader müssen Länge, Breite und Höhe gemessen und miteinander multipliziert werden. Für den Zylinder benötigt man den Durchmesser (bzw. den Radius) und die Höhe des Zylinders, die der Breite des Quaders entspricht. Mit den notwendigen Formeln ergibt sich die Summe der einzelnen Volumina.

Die Aufgabe ist zudem ein schönes Beispiel dafür, dass Schüler bei MathCityMap auch selber zu Autoren werden können. In diesem Fall wurde den Schülern aufgetragen, Aufgaben für jüngere Jahrgangsstufen zu erstellen. Wir sind gespannt auf den Einsatz der Aufgaben!

Autor: Simone Jablonski